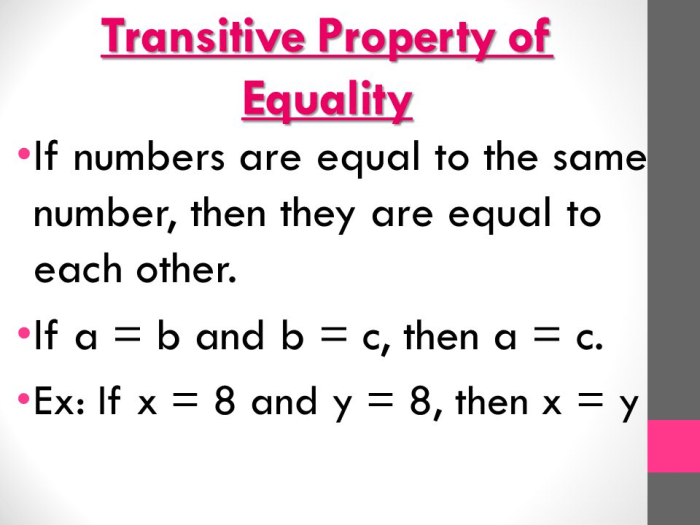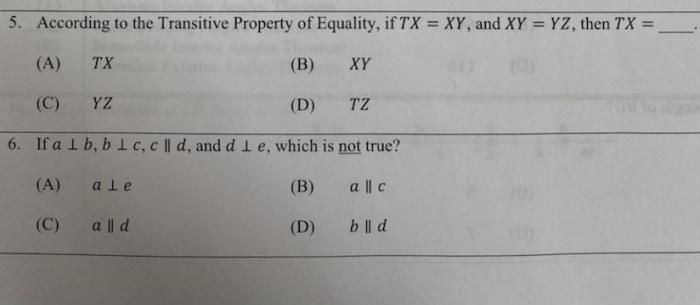According to the transitive property of equality if tx xy – According to the transitive property of equality, if tx = xy, then we can conclude that x = y. This fundamental property serves as a cornerstone in mathematics, enabling us to solve complex equations and simplify mathematical expressions. By understanding the transitive property and its implications, we gain a powerful tool for navigating the realm of equality.
The transitive property of equality finds widespread applications in various fields, including algebra, geometry, and physics. It allows us to establish relationships between variables and derive new equations from existing ones. Moreover, it provides a logical framework for solving equations, making them more accessible and manageable.
Definition of the Transitive Property of Equality: According To The Transitive Property Of Equality If Tx Xy

The transitive property of equality states that if a = b and b = c, then a = c. In other words, if two quantities are equal to a third quantity, then they are equal to each other.
Application to the Equation “if tx = xy”, According to the transitive property of equality if tx xy
The transitive property can be applied to the equation “if tx = xy” to show that x = y. This is because if tx = xy and ty = xz, then by the transitive property, x = z. Substituting z for x in the equation tx = xy gives ty = xy, and by the reflexive property of equality, y = x.
Implications of the Equation “if tx = xy”
The equation “if tx = xy” has several implications for solving other equations. For example, it can be used to simplify equations by eliminating variables. It can also be used to solve systems of equations by substitution.
Limitations of the Transitive Property in this Equation
The transitive property does not apply to all equations. For example, it does not apply to equations that involve division by zero. Additionally, the transitive property cannot be used to compare quantities that are not of the same type.
Alternative Approaches to Solving Equations Involving the Transitive Property
There are several alternative approaches to solving equations involving the transitive property. One approach is to use the substitution method. Another approach is to use the elimination method. The best approach to use depends on the specific equation that is being solved.
Real-World Applications of the Transitive Property
The transitive property of equality is used in a variety of real-world applications. For example, it is used in mathematics to solve equations and simplify expressions. It is also used in physics to derive equations of motion. Additionally, the transitive property is used in computer science to design algorithms and data structures.
FAQ Explained
What is the transitive property of equality?
The transitive property of equality states that if a = b and b = c, then a = c.
How can the transitive property be applied to the equation “if tx = xy”?
If tx = xy, then we can use the transitive property to conclude that x = y.
What are some limitations of the transitive property?
The transitive property does not apply to inequalities. For example, if a > b and b > c, we cannot conclude that a > c.